| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 스위치
- 신경망 첫걸음
- LED
- LED 제어
- Class Activation Map
- function call
- TensorFlow
- file descriptors
- 펌웨어
- Network layer
- 모두를 위한 딥러닝]
- demultiplexing
- 딥러닝
- Switch
- Generalized forward
- Linux
- Transport layer
- 모두를 위한 딥러닝
- Interrupt
- 인터럽트
- 리눅스
- 신경망
- 3분 딥러닝
- 운영체제
- 텐서플로우
- Router
- 디바이스 드라이버
- GPIO
- 밑바닥부터 시작하는 딥러닝
- RDT
Archives
- Today
- Total
건조젤리의 저장소
3-1. How to minimize cost 본문
김성훈 교수님의 강의내용을 정리한 내용입니다.
출처 : http://hunkim.github.io/ml/
모두를 위한 머신러닝/딥러닝 강의
hunkim.github.io

먼저 쉬운 이해를 위해 위의 식을 아래의 식으로 간단하게 나타낸다.
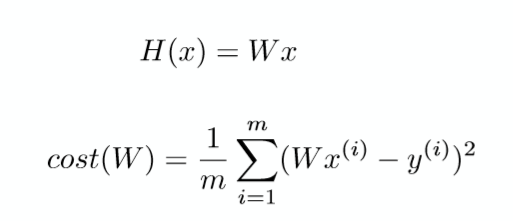
Cost function의 그래프는 어떠한 모양을 가지고 있을까?


위의 그래프에 따르면 W=1 일 경우 최소값을 갖게됨을 알 수 있다.
어떻게 하면 최소값을 찾을 수 있을까?
Gradient descent algorithm (경사 하강법 알고리즘)
- 랜덤한 값으로 초기값을 설정한다.
- Cost function의 미분값을 이용하여 Cost값을 감소시키는 방향으로 값을 약간 수정한다.
- 반복한다.

Cost의 미분값을 사용하므로 쉬운 이해를 위해 값을 약간 수정해보자.

W에 알파값(학습률)과 Cost의 미분값을 곱하여 뺀 후 업데이트 하는 방식을 사용한다.
(기울기가 음수: 앞으로 이동 / 기울기가 양수: 뒤로 이동)
즉 하강하는 방향으로 이동한다.

미분을 계산하면 위의 식과 같다.

초기값의 설정에 따라 찾아가는 최저점이 달라질 수 있다.

이러한 Cost function구조는 초기값이 어디이건 간에 항상 같은 최저점을 찾는다.
'공부 기록 > 모두를 위한 딥러닝 (Basic)' 카테고리의 다른 글
| 4-1. Multi-variable linear regression (0) | 2019.11.06 |
|---|---|
| 3-2. Tensorflow를 이용한 Minimizing Cost확인 (0) | 2019.11.06 |
| 2-2. Tensorflow를 이용한 Linear Regression의 구현 (0) | 2019.11.06 |
| 2-1. Linear Regression (0) | 2019.11.06 |
| 1. Machine Learning Basics (모두를 위한 딥러닝 정리) (0) | 2019.11.06 |
Comments




